Half the parents I know posted this video when it came out, as a blow against the Common Core. In case you didn't watch it, here is the gist. There is a math problem. The kids are expected to use a method that the mother in the video deems ridiculous.
Mr.Yamata's class has 18 students.If the class counts around by a number and ends with 90. What number did they count by?
Most reasonable people would simply divide 90 by 18 to get 5. However, in this scenario, the kids are expected to draw 18 circles and make hash marks rather than treat this as a division problem. How ridiculous is this? Turning a one step quickie division problem into a 108 step problem. What is the point of that? Let's throw out all the skills that are being taught and go complain to the school board.
The point of that is it teaches procedural knowledge. It gives them an alternate method to get to the answer. This may not seem important when we are talking about a simple division problem, but what if the problem is more complex?
In an Educational Psychology class I am taking, we were given a seemingly simple problem. Here we are all graduate students. The majority of us have taken statistics in some form. All but 3 of us took the NYS Math Regents Sequence. There were even 2 math teachers in the room. So here is the problem:
You are making a fruit salad. There are 5 fruits you can use - apples, strawberries, grapes, bananas, oranges. The bowl you are using will only hold the salad if you limit it to 3 fruits. How many different combinations are possible?
A. 10
B. 15
C. 20
D. 30
E. 120
The discussion begins. "Don't we use 5! and multiply out 5*4*3*2*1?" "No, you would would do that if the order were important." "I think she is right, but you have to divide it by something." "But what? What do you divide by? Do you remember the formula?"
Then finally someone suggest we write it out. A S G B O. Apple Strawberry Grape and so on.
ASG
ASB
ASO
AGB
AGO
ABO
SGB
SGO
SBO
GBO
So there are 10 combinations. We as graduate students used a process very similar to drawing circles and making hash marks because not one of us remembered the formula to figure out combinations and somehow we got to the right answer. Yes, if we could have recalled the formula it may have been quicker. Does that make our method less valid?
The point of the seemingly ridiculous exercise talked about in the video is to give the kids an alternate way to do the problem. You can't always recall every formula for each problem by wrote. Occasionally you may need to figure something out using a less than ideal method, and that is okay. In this era of high stakes testing, it is important for kids to understand that there may be more than one method to get to the correct answer. You can also use a method like this to double check your work. So please, do all of the 4th grade math teachers a favor and cut them some slack. They are teaching skills that will be useful in a variety of situations, even when you can't remember the formula.
If you are curious the way you would do this problem follows.
5C3
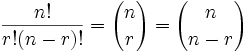
n=5
r=3
(5*4*3*2*1)
(3*2*1)(2*1)
120
(6)(2)
120/12= 10
